오늘은 퀀트투자에서 주로 활용하는 평균회귀전략 mean reversion strategy을 살펴보도록 하겠습니다
퀀트투자에서 평균 회귀 전략(mean reversion strategy)은 주가나 다른 금융 자산의 가격이 일시적으로 일어난 변동 이후에 평균적인 가격 수준으로 회귀하는 경향이 있다는 가설에 기초한 투자 전략입니다.

이 전략은 주식, 채권, 화폐, 상품 등 다양한 투자 자산에서 사용합니다.
평균 회귀 전략은 일반적으로 시계열 분석 기법을 사용하여, 특정 금융 자산의 가격이 일정 기간 동안 평균 수준에서 벗어날 때 매수 또는 매도하도록 결정합니다. 이는 가격이 일시적으로 상승하거나 하락할 때, 가격이 다시 원래의 평균 수준으로 회귀할 가능성이 높다는 가정하에 실시합니다.
평균 회귀 전략은 단기적인 가격 변동에서 수익을 추구하는 것보다는, 장기적인 투자 수익을 목표로 하는 경우가 많습니다. 따라서 이 전략은 일반적으로 저위험, 중수익의 투자 전략으로 평가됩니다.
그러나, 평균 회귀 전략도 모든 금융 자산에 적용될 수 있는 것은 아니며, 시장의 상황과 환경에 따라 성과가 크게 달라질 수 있습니다. 따라서 이 전략을 적용할 때는 적절한 리스크 관리와 다양한 전략의 활용이 필요합니다.
그러면 구체적으로 퀀트투자의 평균회귀전략 mean reversion strategy에 대해서 자세히 살펴보도록 하겠습니다.
퀀트투자에서 평균회귀전략 mean reversion strategy이 중요한 이유는 다음과 같습니다
퀀트투자에서 평균 회귀 전략이 중요한 이유는 간단합니다. 평균 회귀 전략의 알고리즘은 다른 투자전략에 비해 상대적으로 간단하지만, 효과적인 투자 전략이기 때문입니다.
퀀트 투자에서는 대부분의 의사 결정이 컴퓨터 알고리즘에 의해 이루어지며, 이는 정교하고 복잡한 모델을 활용하여 데이터를 분석하는 것을 통해 이루어집니다.
결국 퀀트투자의 알고리즘은 과거의 데이터를 활용하여 미래를 예측하는 것입니다. 이러한 투자 알고리즘 모델은 결국 과거 데이터를 기반으로 의사결정을 내릴 수밖에 없습니다. 그러다보니 과거의 데이터를 기반으로 투자전략을 결정하는 평균 회귀 전략이 특히 유용한 것입니다.
평균 회귀 전략은 과거 데이터를 기반으로 현재의 가격과 비교하여 가격이 어디에 위치해 있는지 파악하고, 그것이 높거나 낮은지를 판단하여 투자를 결정합니다. 이는 과거 데이터를 이용하여 현재 시장의 트렌드와 패턴을 분석하고, 향후 시장의 동향을 예측하는 데 도움이 되며, 모델의 성능을 개선하는 데 기여합니다.
또한, 평균 회귀 전략은 단기적인 가격 변동보다는 장기적인 투자 수익을 추구하는 전략이므로, 퀀트 투자에서 안정적인 수익을 추구하는 데 효과적입니다. 따라서, 퀀트 투자에서 평균 회귀 전략은 매우 중요하며, 다양한 퀀트 전략과 함께 사용되는 경우도 많습니다.
퀀트투자에서 평균회귀전략 mean reversion strategy의 절차는 다음과 같습니다
평균 계산
- 시계열 데이터를 수집하고 이를 기반으로 주가의 평균을 계산합니다.
- 이 때, 간단한 평균(mean) 또는 가중 평균(weighted mean)을 사용할 수 있습니다.
표준 편차 계산
- 주가의 분산을 계산하고 이를 표준 편차로 변환합니다.
- 이는 주가의 변동성을 계산하는 데 사용됩니다.
매매 시점 결정
- 현재 주가와 평균 가격을 비교하여 주가가 평균 가격보다 높은 경우 판매하고, 주가가 평균 가격보다 낮은 경우 매입합니다.
- 이때, 표준 편차를 기반으로 주가의 변동성에 따라 매매 시점을 조절할 수 있습니다.
리밸런싱
- 일정 기간마다 포트폴리오를 리밸런싱하여 매매 규칙을 업데이트합니다.
- 이때, 리밸런싱 주기와 매매 규칙을 어떻게 업데이트할지 결정해야 합니다.
평균 회귀 전략은 간단하면서도 효과적인 전략으로, 다양한 변형이 가능합니다. 예를 들어, 여러 종목을 포함하는 포트폴리오를 만들어 리밸런싱하는 방식도 있습니다. 이때, 각 종목의 평균 가격과 표준 편차를 계산하여 매매 시점을 결정합니다.
일반적인 평균회귀전략의 파이썬 코드 예시는 다음과 같습니다.
import pandas as pd
import numpy as np
# 평균 회귀 전략 함수
def mean_reversion(df, lookback, buy_threshold, sell_threshold):
# 주가 이동평균 계산
ma = df['Close'].rolling(lookback).mean()
# 주가 이동평균 대비 수익률 계산
returns = df['Close'] / ma - 1
# 매수/매도 시그널 계산
buy_signal = returns < -buy_threshold
sell_signal = returns > sell_threshold
# 매수/매도 포지션 계산
position = np.zeros(len(df))
position[buy_signal] = 1
position[sell_signal] = -1
# 포트폴리오 수익률 계산
strategy_returns = position * df['Returns']
# 최종 수익률 반환
return strategy_returns.cumsum()
그러면 평균회귀전략 중 고빈도 데이터를 활용하는 단기 평균회귀 전략 Short-term Mean-reversion on High Frequency Data과 다중 진입 시점을 활용하는 장기 평균회귀 전략 Long-term Mean-reversion with Multiple Entry Points에 대해서 조금 더 자세히 살펴보겠습니다.
고빈도 데이터를 활용하는 단기 평균회귀 전략 Short-term Mean-reversion on High Frequency Data은 다음과 같습니다.
고빈도 데이터를 활용하는 단기 평균회귀 전략"Short-term Mean-reversion on High Frequency Data" 전략은 고빈도 데이터를 이용하여 단기적인 평균회귀 현상을 이용한 전략입니다. 이 전략은 주식, 선물, 화폐, 지수 등의 다양한 시장에서 적용할 수 있습니다.

이 전략은 기본적으로 다음과 같은 원리로 동작합니다. 우선, 일정 기간 동안 (예: 30분, 1시간 등) 시장에서 상승한 종목들을 골라냅니다. 그리고 이 종목들의 가격이 지금까지 상승했던 평균 가격보다 높아진 경우 매도합니다. 이후, 일정 기간 동안 시장에서 하락한 종목들을 골라냅니다. 그리고 이 종목들의 가격이 지금까지 하락했던 평균 가격보다 낮아진 경우 매수합니다.
이 전략은 주로 높은 주기적 리밸런싱을 통해 구현됩니다. 즉, 일정 기간마다 평균 가격을 다시 계산하고, 해당 기간에서 상승한 종목과 하락한 종목을 다시 선별하여 매매합니다. 이를 통해 평균 가격의 변화에 따라 적극적으로 매매하여 수익을 얻습니다.
고빈도 데이터를 활용하는 단기 평균회귀 전략 "Short-term Mean-reversion on High Frequency Data" 전략은 매우 빠른 시간 간격으로 데이터를 수집하고 분석하므로, 실시간 데이터 수집과 분석 기술이 필요합니다. 또한, 퀀트 투자에서는 백테스트를 통해 전략의 성과를 검증하므로, 과거 데이터를 이용하여 백테스트를 수행할 수 있는 백테스트 플랫폼도 필요합니다.
고빈도 데이터를 활용하는 단기 평균회귀 전략은 다음과 같은 알고리즘들을 활용합니다.
Z-Score 알고리즘
- 과거의 가격 데이터를 이용하여 평균과 표준편차를 계산합니다.
- 현재 가격이 평균과의 거리를 표준편차로 나눈 값을 Z-Score로 정의합니다.
- Z-Score가 일정 수준 이상이 되면 매도 포지션을, 일정 수준 이하가 되면 매수 포지션을 취합니다.
Bollinger Bands 알고리즘
- 과거의 가격 데이터를 이용하여 이동평균선과 표준편차를 계산합니다.
- 이동평균선을 중심으로 상위/하위 표준편차 범위를 나타내는 Bollinger Bands를 그립니다.
- 현재 가격이 Bollinger Bands의 상/하단 경계를 넘어가면 매도 포지션을, 중앙선을 넘어가면 매수 포지션을 취합니다.
Kalman Filter 알고리즘
- Kalman Filter는 시간에 따라 변화하는 값을 추적하는데 사용됩니다.
- 과거의 가격 데이터를 이용하여 상태 추정치와 오차 공분산을 계산합니다.
- 현재 가격이 추정치와 비교하여 일정 기준치 이상으로 상승/하락하면 매도/매수 포지션을 취합니다.
고빈도 데이터를 활용하는 단기 평균회귀 전략"Short-term Mean-reversion on High Frequency Data" 전략에서 Z-Score 알고리즘의 Python 언어로 작성된 예시 코드는 다음과 같습니다.
import numpy as np
import pandas as pd
import yfinance as yf
# Set parameters
symbol = "AAPL"
lookback = 20
threshold = 1.5
# Download historical data
data = yf.download(symbol, period="1d", interval="1m")
# Calculate rolling mean and standard deviation
rolling_mean = data["Close"].rolling(window=lookback).mean()
rolling_std = data["Close"].rolling(window=lookback).std()
# Calculate Z-Score
z_score = (data["Close"] - rolling_mean) / rolling_std
# Define entry and exit signals based on Z-Score threshold
entry_signal = z_score < -threshold
exit_signal = z_score > 0
# Calculate positions based on entry and exit signals
positions = pd.Series(0, index=data.index)
positions[entry_signal] = 1
positions[exit_signal] = 0
positions = positions.ffill().fillna(0)
# Calculate returns based on positions and market price
market_returns = data["Close"].pct_change()
strategy_returns = market_returns * positions.shift(1)
cumulative_strategy_returns = (1 + strategy_returns).cumprod()
# Plot cumulative returns
cumulative_strategy_returns.plot(figsize=(10, 6))
이어서 다중 진입 시점을 활용하는 장기 평균회귀 전략 Long-term Mean-reversion with Multiple Entry Points을 살펴보겠습니다.
다중 진입 시점을 활용하는 장기 평균회귀 전략 Long-term Mean-reversion with Multiple Entry Points 은 다음과 같습니다.
다중 진입 시점을 활용하는 장기 평균회귀 전략 "Long-term Mean-reversion with Multiple Entry Points" 전략은 장기적인 평균회귀 현상을 이용하여 전략을 수립하는 것을 목표로 합니다. 이전의 가격 데이터를 분석하여 시장에서 일어나는 평균회귀 현상을 파악하고, 이를 기반으로 매매 전략을 수립합니다.

이 전략은 다양한 종목, 예를 들면 주식, 선물, 화폐, 지수 등에서 적용 가능합니다. 전략의 기본 원리는 다음과 같습니다. 일정 기간 (예: 1년) 동안 종목의 가격 데이터를 수집한 후, 이를 이용하여 평균 가격을 계산합니다. 그리고 현재 시장에서 거래되는 가격이 평균 가격보다 높아지면 매도, 평균 가격보다 낮아지면 매수하는 전략입니다.
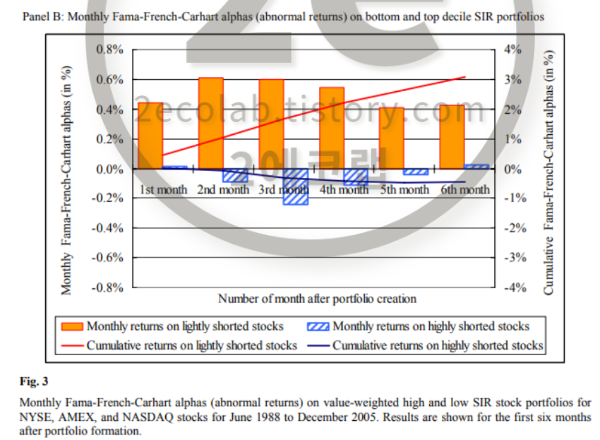
다중 진입 시점을 활용하는 장기 평균회귀 전략 "Long-term Mean-reversion with Multiple Entry Points" 전략은 평균회귀 현상을 이용하여 전략을 구성하고 있기 때문에, 매수/매도 타이밍이 매우 중요합니다. 따라서, 이전 데이터를 분석하여 적절한 매수/매도 포인트를 정확하게 파악해야 합니다. 또한, 한 번의 매수/매도로 이루어지는 경우도 있지만, 여러 번의 매수/매도 포인트를 설정하여 차등 매수/매도를 수행하기도 합니다.
이전 데이터를 이용하여 전략을 구성하기 때문에, 퀀트 투자에서는 백테스트를 통해 전략의 성과를 검증합니다. 백테스트는 과거의 데이터를 이용하여 전략을 수행하고, 그 결과를 분석하여 실제 시장에서 적용할 수 있는 전략을 도출하는 것입니다.
다중 진입 시점을 활용하는 장기 평균회귀 전략은 다음과 같은 알고리즘들을 활용합니다.
- 선형 회귀 분석: 회귀 분석을 사용하여 주가와 시간 간의 관계를 분석하고 추세를 파악합니다. 이를 기반으로 평균 회귀 전략을 수행합니다.
- 이동평균(Moving Average): 이동평균을 사용하여 최근 일정 기간의 주가 평균을 계산하고, 이를 기준으로 주가의 추세를 파악합니다. 이동평균을 기반으로 평균 회귀 전략을 수행합니다.
- 볼린저 밴드(Bollinger Bands): 주가의 이동평균과 일정 수준의 표준 편차를 기반으로 한 상한선과 하한선을 계산하여, 주가의 상승과 하락 구간을 파악합니다. 이를 기반으로 평균 회귀 전략을 수행합니다.
- 상대강도지수(Relative Strength Index, RSI): 일정 기간 동안 주가 상승률과 하락률의 평균을 계산하여, 주가의 상승과 하락 강도를 측정합니다. 이를 기반으로 평균 회귀 전략을 수행합니다.
다중 진입 시점을 활용하는 장기 평균회귀 전략 Long-term Mean-reversion with Multiple Entry Points 전략에서 선형 회귀 분석 알고리즘의 Python 예시 코드는 다음과 같습니다.
import pandas as pd
import numpy as np
import yfinance as yf
from sklearn.linear_model import LinearRegression
# set the parameters
symbol = 'AAPL'
lookback_period = 200
entry_points = [0.5, 1, 1.5]
exit_point = 0
# download the historical data for the stock
data = yf.download(symbol, start='2010-01-01')
# calculate the 200-day moving average
ma = data['Adj Close'].rolling(window=lookback_period).mean()
# calculate the difference between the price and the 200-day moving average
data['diff'] = data['Adj Close'] - ma
# create a new DataFrame for the linear regression analysis
regression_data = pd.DataFrame(columns=['mean_diff', 'diff_today'])
# loop through the price data to populate the regression_data DataFrame
for i in range(lookback_period, len(data)):
mean_diff = np.mean(data['diff'][i-lookback_period:i])
diff_today = data['diff'][i]
regression_data = regression_data.append({'mean_diff': mean_diff, 'diff_today': diff_today}, ignore_index=True)
# perform linear regression on the regression_data DataFrame
regression_model = LinearRegression()
regression_model.fit(regression_data[['mean_diff']], regression_data['diff_today'])
slope = regression_model.coef_[0]
intercept = regression_model.intercept_
# print the slope and intercept of the regression line
print('Slope:', slope)
print('Intercept:', intercept)예시로 살펴본 코드는 모두 Yahoo Finance API를 사용하여 AAPL 주식의 과거 가격 데이터를 다운로드하여 각각의 평균회귀전략을 수행하는 코드입니다.
이 코드는 참고용 예시라는 점을 기억하시기 바랍니다.
오늘은 퀀트투자에서 주요 전략으로 사용하는 평균회귀전략 mean reversion strategy에 대해서 총정리하고, 특히 고빈도 데이터를 활용하는 단기 평균회귀 전략 Short-term Mean-reversion on High Frequency Data과 다중 진입 시점을 활용하는 장기 평균회귀 전략 Long-term Mean-reversion with Multiple Entry Points도 살펴보았습니다.
어디까지나 투자는 본인의 책임에 따른 것이며, 퀀트투자 역시 알고리즘 트레이딩의 일종으로 최근 인공지능 열풍이 불면서 큰 인기를 끌고 있지만, 사실은 이러한 알고리즘에 의한 투자는 꽤 오래전부터 등장했다는 점을 꼭 기억하셔야 합니다.
인공지능이 무조건 투자 수익을 높일 것이라는 환상을 가져서는 안될 것이며, 퀀트투자 역시 알고리즘에 기반한 트레이딩이라는 것을 꼭 기억하셨으면 합니다.
이상으로 평균회귀전략 mean reversion strategy 총정리 포스팅을 마칩니다. 감사합니다.
'인공지능과 경제' 카테고리의 다른 글
| 퀀트가치투자전략 Quantitative value investing 총정리 (1) | 2023.03.08 |
|---|---|
| 모멘텀전략 Momentum Strategy 총정리 (2) | 2023.03.07 |
| 퀀트투자 Quant investing 총정리 (6) | 2023.03.05 |
| 챗GPT 탐구 총정리 (0) | 2023.02.19 |
| ChatGPT를 통해 알아본 블로그 운영법 (0) | 2023.02.16 |


댓글